Изучаем матрицы трансформаций в CSS
- Введение
- Что такое матрица?
- Трансформации и системы координат
- Расчет трансформации: математика матриц и векторов
- Составные трансформации с помощью матриц
Введение
Матричные функции — matrix() and matrix3d() — две самые головоломные в плане понимания вещи в CSS3-трансформациях. В большинстве случаев, ради простоты и ясности, вы будете пользоваться функциями вроде rotate() и skewY(). Но всё же за каждой трансформацией скрывается эквивалентная матрица. Полезно хоть слегка понимать, как они работают, так что давайте взглянем.
CSS-трансформации «растут» из линейной алгебры и геометрии. Хотя продвинутая математическая подготовка будет весьма не лишней, понять матричные функции можно и без нее. Но вы должны быть хорошо знакомы с CSS-трансформациями. Иначе — читайте про эффекты переходов CSS3 и 2D-трансформации.
В этой статье я охвачу как матрицы 3 на 3, используемые для двумерных трансформаций, так и матрицы 4 на 4 для трехмерных.
Заметьте, что на момент этой публикации Opera не поддерживает трехмерных трансформаций. Я включила двумерный matrix()-эквивалент, где возможно.
В этой статье я также пользуюсь беспрефиксными версиями свойств transform. На практике эти свойства всё еще экспериментальны и могут измениться. Пока они не утверждены окончательно, добавляйте в свой CSS-код версии с префиксом (напр., -o-transform).
Что такое матрица?
Матрица — это прикольный математический термин для прямоугольного массива чисел, символов или выражений
(см. рис. 1). У матриц множество математических и научных применений. Физики, например, используют их при изучении квантовой механики. В области компьютерной графики они используются для вещей типа — внезапно! — линейных трансформаций и проекции трехмерных изображений на двумерный экран. Это и есть то, что делают матричные функции: matrix() позволяет нам создавать линейные трансформации, а matrix3d()дает возможность создавать иллюзию трехмерности в двух измерениях с помощью CSS.
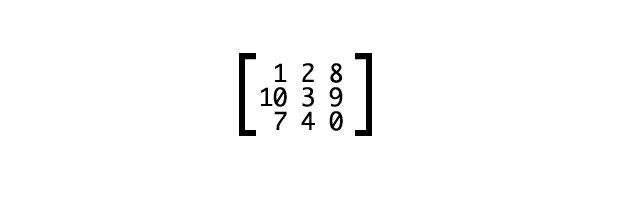
Рис. 1. Пример матрицы
Мы не будем далеко забредать в глубины продвинутой алгебры. Вы должны быть знакомы с декартовой системой координат. Можете также освежить в памяти, как перемножать матрицы и векторы (либо воспользуйтесь калькулятором, типа предлагаемого Bluebit.gr).
Важный для понимания момент — то, что трансформация умножает матрицу на координаты точки (или точек), выраженные в виде вектора.
Трансформации и системы координат
Сначала поговорим о системах координат. Каждая область просмотра документа является системой координат. Левый верхний угол — ее начало, с координатами (0,0). Значения увеличиваются вправо по оси X и вниз по оси Y. Ось Z определяет кажущееся расстояние до зрителя в случае 3D-трансформаций. Бо́льшие значения — предметы ближе и крупнее, меньшие значения — мельче и дальше.
Когда трансформация применяется к объекту, она создает локальную систему координат. По умолчанию начало локальных координат — точка (0,0) — лежит в центре объекта, или на 50% ширины и 50% высоты (рис. 2).
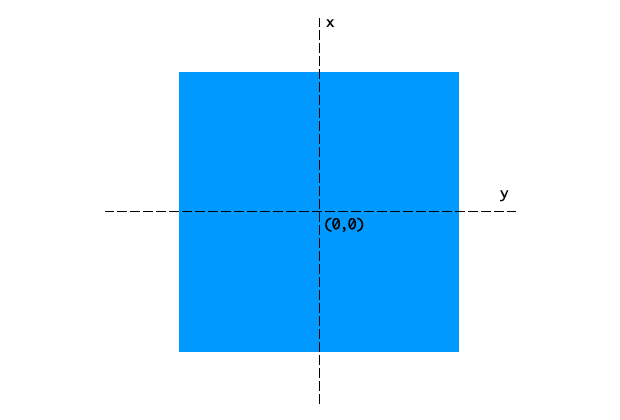
Рис.2. Локальная система координат
Мы можем изменить начало локальной системы координат подгонкой свойства transform-origin (рис. 3). Задание transform-origin: 50px 70px;, например, помещает начало координат в 50 пикселях от левого края объекта и в 70 пикселях от его верха. Трансформации каждой точки в локальной системе координат объекта рассчитываются относительно этого начала.
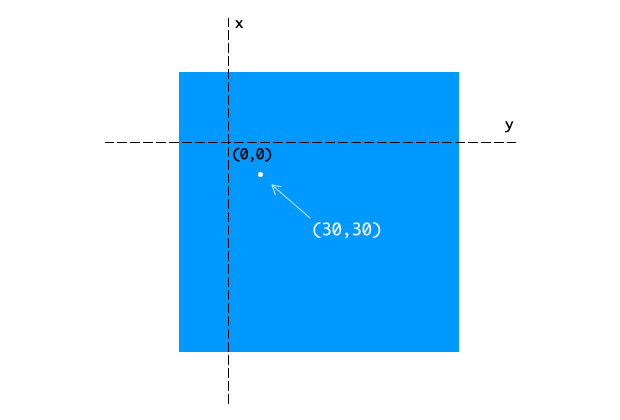
Рис. 3. Локальная система координат, с началом в точке (50px,70px). Также показана точка (30px,30px).
Браузеры делают за вас эти вычисления каждый раз, когда вы применяете трансформацию. Вам нужно лишь знать, какие аргументы могут помочь достичь нужного вам эффекта.
Расчет трансформации: математика матриц и векторов
Взглянем на пример с использованием матрицы 3 на 3 для расчета двумерной трансформации (рис. 4). Матрица 4 на 4, используемая для трехмерных трансформаций, работает так же, с дополнительными числами для добавочной оси Z.
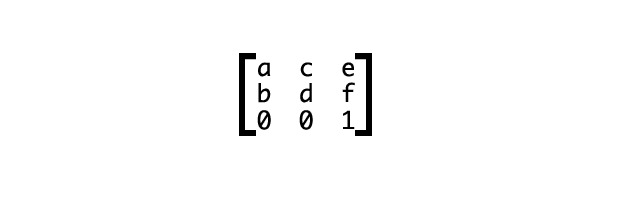
Рис. 4. Матрица двумерной CSS-трансформации
Мы можем записать это как transform: matrix(a,b,c,d,e,f), где буквы от a до f — числа, определяемые типом трансформации, которую мы хотим применить. Матрицы — это рецепты тех видов трансформации, которые мы хотим применить. Это станет чуть понятнее, когда мы рассмотрим несколько примеров.
Когда мы применяем двумерную трансформацию, браузер умножает матрицу на вектор [x, y, 1]. Значения x и y — координаты конкретной точки в локальном пространстве координат.
Чтобы найти координаты после трансформации, мы умножаем каждый элемент каждой строки матрицы на соответствующую ему строку вектора. Затем складываем произведения (рис. 5).
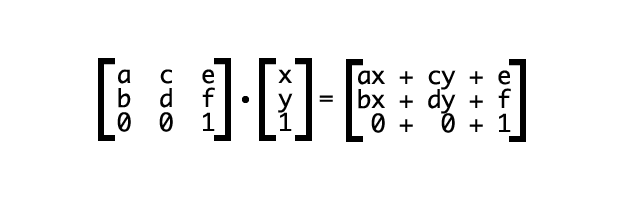
Рис. 5. Умножение матрицы на вектор
Я знаю, что это выглядит как куча бессмысленных цифр и букв. Но, как отмечено выше, у каждого типа трансформаций — своя собственная матрица. Рис. 6 показывает матрицу для трансформации сдвига.
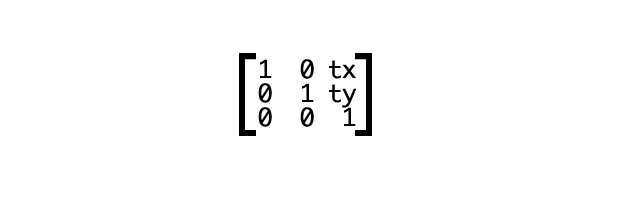
Рис. 6. Матрица сдвига
Значения tx и ty — значения, на которые должно быть сдвинуто начало координат. Мы также можем представить это с помощью вектора [1 0 0 1 tx ty]. Этот вектор служит аргументом для функции matrix(), как показано ниже.
#mydiv{
transform: matrix(1, 0, 0, 1, tx, ty);
}Давайте трансформируем объект, левый верхний угол которого совпадает с левым верхним углом области просмотра (Рис. 7). Его глобальные координаты равны (0,0).
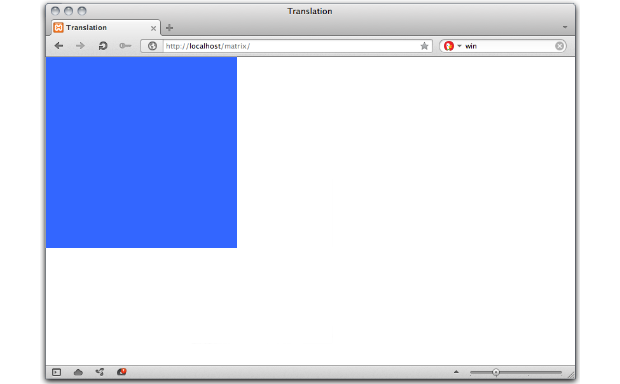
Рис. 7. Объект с глобальными координатами (0,0).
Мы переместим этот объект на 150 пикселей по осям x и y, используя начало координат трансформации по умолчанию. Ниже приведен CSS для этой трансформации.
#mydiv{
transform: matrix(1, 0, 0, 1, 150, 150);
}Кстати, это эквивалентно transform: translate(150px,150px). Давайте рассчитаем результат этой трансформации для точки с координатами (220px,220px) (Рис. 8).
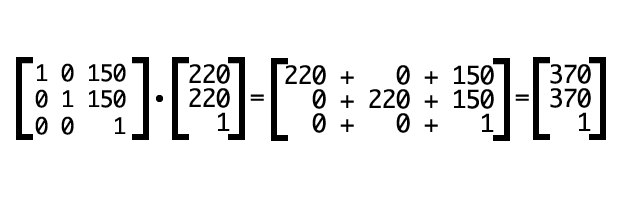
Рис. 8. Вычисление трансформации сдвига.
Трансформации задают соответствие координатам и расстояниям в локальной системе координат объекта предыдущей системе координат. То, где точка отобразится в области просмотра, зависит от примененного при трансформации сдвига от начальной точки объекта. В этом примере наша точка с координатами (220px,220px) теперь отображается в точке (370px,370px). Прочие координаты в границах нашего объекта тоже сместились на 150 пикселей вправо и на 150 пикселей вниз (рис. 9).
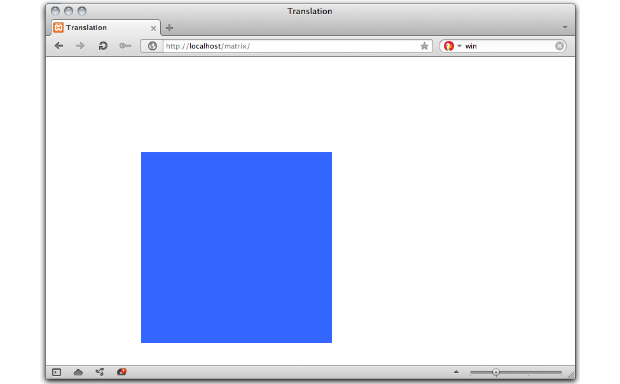
Рис. 9. Наш объект после применения трансформации.
Матрица сдвига — особый случай. Она как аддитивна, так и мультипликативна. Более простым решением было бы просто прибавить значение сдвига к значениям x- и y-координат нашей точки.
Расчет трехмерной трансформации
Выше мы рассмотрели матрицу переноса 3 на 3. Давайте возьмем другой пример, с использованием матрицы 4 на 4 для масштабирования (рис. 10).
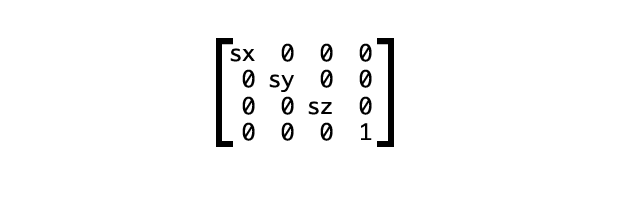
Рис. 10. Матрица 4 на 4 для масштабирования.
Здесь sx, sy и sz представляют масштабные коэффициенты по каждой оси. С функцией matrix3d это примет такой вид: transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1).
Будем продолжать с тем же объектом, что раньше. Уменьшим его масштаб по осям x и y с помощью функции matrix3d(), как показано ниже.
#mydiv{
transform: matrix3d(.8, 0, 0, 0, 0, .5, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1);
}Это эквивалентно transform: scale3d(0.8, 0.5, 1). Поскольку мы масштабируем только по осям x и y (получая 2D-трансформацию), мы могли бы использовать также transform: matrix(.8, 0, 0, .5, 0, 0) либо scale(.8,.5). Результат трансформации виден на рис. 11.
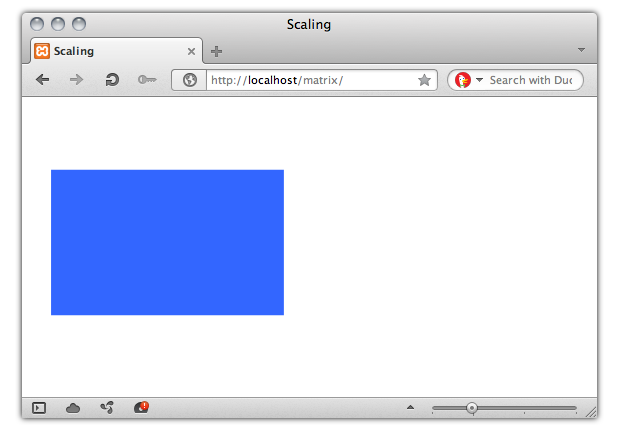
Рис. 11. Объект 300 на 300 пикселей после применения трансформации масштабирования.
Если умножить эту матрицу на координатный вектор [150,150,1] (рис. 12), мы получим такие новые координаты нашей точки: (120,75,1).
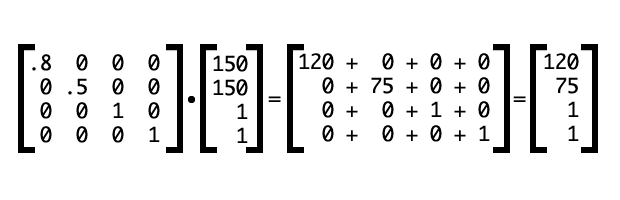
Рис. 12: Вычисление трансформации масштабирования.
Где взять значения матриц
Значения матриц для каждой функции трансформации приведены как в спецификации Scalable Vector Graphics, так и в спецификации CSS Transforms.
Составные трансформации с помощью матриц
Наконец, давайте рассмотрим, как создать составную трансформацию — трансформацию, эквивалентную применению нескольких функций трансформации одновременно. Ради простоты ограничимся двумя измерениями. Это значит, что мы будем использовать матрицу трансформации 3 на 3 и функцию matrix(). Этой трансформацией мы повернем наш объект на 45° и увеличим его масштаб в 1,5 раза от исходного размера.
Матрица поворота, выраженная в виде вектора — [cos(a) sin(a) -sin(a) cos(a) 0 0], где a — угол. Для масштабирования понадобится матрица [sx 0 0 sy 0 0]. Чтобы объединить их, умножим матрицу поворота на матрицу масштабирования, как показано на рис. 13 (синус и косинус 45° оба равны 0.7071).
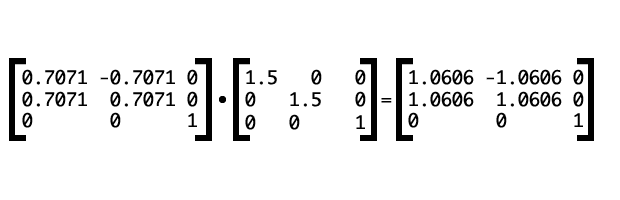
Рис. 13: Вычисление матрицы составной трансформации.
В CSS это будет выглядеть так: transform: matrix(1.0606, 1.0606, -1.0606, 1.0606, 0, 1). Рис. 14 показывает результат после применения трансформации.
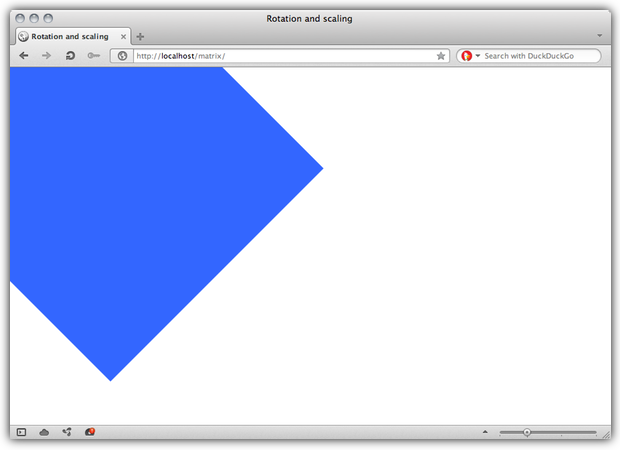
Рис. 14: Наш объект 300 на 300 пикселей после масштабирования и поворота.
Теперь рассчитаем новые координаты в области просмотра для точки (298,110), как показано на рис. 15.
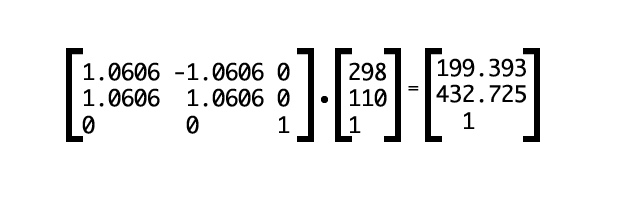
Рис. 15. Применение трансформации.
Новыми координатами нашей точки будут (199.393px,432.725px).
Узнать больше
Надеюсь, эта статья немного приподняла завесу тайны над CSS-трансформациями. Если ей это не удалось, попробуйте обратиться к ресурсам ниже.
- Матрица (математика) в Википедии
- Объяснение матрицы трансформации во Flash 8 (автор — Senocular)
- Трансформации на сайте WolframMathWorld
Текстура матрицы на обложке Патрика Хосли.
This article is licensed under a Creative Commons Attribution 3.0 Unported license.
Comments
No new comments accepted.